Tìm hiểu code anime lands simulator Mới Nhất và cách nhập code anime lands simulator
Share Code
September 7, 2023
Bạn có muốn tìm hiểu về code anime lands simulator Mới Nhất và cách nhập code trong trò chơi này?…

Tổng hợp code Arena Mania mới nhất tháng 8/2023
Share Code
September 7, 2023
Bí mật tối quan trọng mà game thủ không thể bỏ qua – code Arena Mania mới nhất! Trên bài viết…
Tổng hợp code Arch Piece mới nhất năm 2023 và hướng dẫn nhập code
Share Code
September 7, 2023
Bạn có muốn biết những thông tin mới nhất về code Arch Piece mới nhất năm 2023? Hãy đọc bài…

Cập nhập danh sách code Arcana Tactics mới nhất tháng 8/2023
Share Code
September 7, 2023
Bí mật về code Arcana Tactics mới nhất đang chờ đón bạn! Hãy cùng tamquoccola khám phá những mã code hấp…

Code Arcana Roblox mới nhất và cách nhập code
Share Code
September 7, 2023
Trong bài viết này, tôi sẽ chia sẻ với bạn toàn bộ danh sách mã code Arcana Roblox mới nhất…

Code Arcade Hunter mới nhất năm 2023 và cách nhập code
Share Code
September 7, 2023
Để tăng khả năng sức mạnh cho nhân vật trong trò chơi Arcade Hunter, tôi sẽ trình bày cho các…

TỔNG HỢP CÁC MÃ CODE APOCALYPTIC RISE OF HERO
Share Code
September 7, 2023
Hãy cùng tôi khám phá những mã code apocalyptic rise of hero mới nhất để trải nghiệm chuỗi sự kiện…

Code A Piece game mới nhất năm 2023
Share Code
September 7, 2023
Bạn đang tìm kiếm mã code a piece mới nhất miễn phí?.Hãy cùng tamquoccola theo dõi bài viết dưới đây…

Code A One Piece game mới nhất năm 2023 và cách nhập
Share Code
September 7, 2023
Hãy đón chờ mã Code A One Piece game mới nhất, nơi bạn sẽ được trải nghiệm một cuộc phiêu…

Danh sách code Ảo Linh Sư mobile mới nhất 2023 và cách nhập code
Share Code
September 7, 2023
Khám phá danh sách mã code Ảo Linh Sư mobile mới nhất 2023 và bí quyết nhập code để có…

Danh sách các code Ant Legion mới nhất năm 2023
Share Code
September 7, 2023
Hãy khám phá danh sách các mã code Ant Legion mới nhất, với phiên bản mới nhất được tung ra…

Code Anime Wrecking Simulator MỚI NHẤT và hướng dẫn dùng code
Share Code
September 6, 2023
Bạn đang tìm kiếm mã Code Anime Wrecking Simulator MỚI NHẤT? Trong bài viết này, tamquoccola sẽ cung cấp cho…

Tổng hợp code Anime World Tower Defense mới nhất và hướng dẫn nhận code
Share Code
September 6, 2023
Bạn đang tìm kiếm thông tin về Code Anime World Tower Defense mới nhất? Với Anime World Tower Defense, bạn…
Code Anime Weapon Simulator Mới Nhất: Bạn đã từng muốn sở hữu những loại vũ khí huyền thoại trong anime…
Code Anime Warriors Simulator mới nhất và hướng dùng code
Share Code
September 6, 2023
Bạn đang tìm kiếm các code Anime Warriors Simulator mới nhất? Đây là một trong những trò chơi trên Roblox…
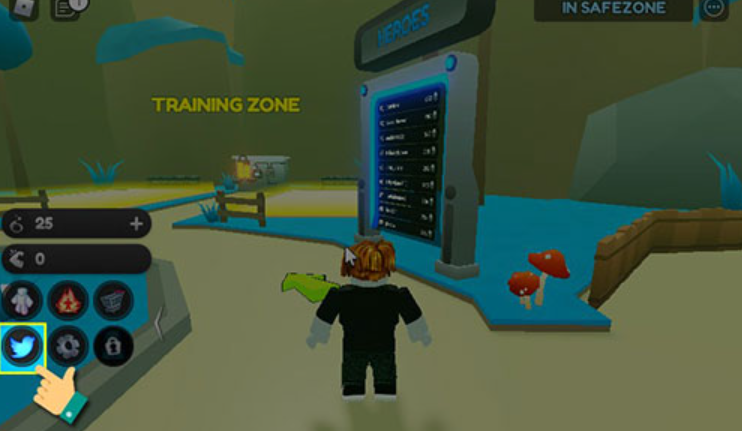
Code Anime Training Simulator Mới Nhất và hướng dẫn dùng Code
Share Code
September 6, 2023
Bạn đang tìm kiếm những Code Anime Training Simulator Mới Nhất? Bạn muốn có thêm tiền vàng, gem, coin, cash,…

Code Anime Swords Simulator MỚI NHẤT 2023 và cách nhập
Share Code
September 6, 2023
Code Anime Swords Simulator MỚI NHẤT – Anime Swords Simulator là một trò chơi trong Roblox, nơi bạn có thể…

Tổng hợp các code Anime Story mới nhất và hướng dẫn sử dụng code
Share Code
September 6, 2023
Với Code Anime Story mới nhất, bạn sẽ có cơ hội nhận được các loại tiền tệ quan trọng như…

Khám phá những Code Anime Souls Simulator mới nhất và cách nhập
Share Code
September 6, 2023
Code Anime Souls Simulator mới nhất: Anime Souls Simulator là một tựa game hành động độc đáo trên nền tảng…

Tổng hợp code anime showdown Mới Nhất và hướng dẫn cách dùng code
Share Code
September 6, 2023
Bạn muốn biết mã code Anime Showdown mới nhất? Hãy tiếp tục đọc bài viết này để cập nhật thông…

Khám phá code anime rising fighting mới nhất và cách nhập code anime rising fighting
Share Code
September 6, 2023
Bạn muốn khám phá mã code anime rising fighting mới nhất và cách nhập mã code cho trò chơi anime…

Khám phá code anime race clicker mới nhất và cách nhập code anime race clicker
Share Code
September 6, 2023
Bạn đã từng nghe về anime race clicker và muốn khám phá phiên bản mới nhất của trò chơi này?…

Khám phá code anime punching simulator mới nhất và cách nhập code anime punching simulator
Share Code
September 6, 2023
Bạn muốn khám phá code anime punching simulator mới nhất và biết cách nhập chúng? Các mã code này là…
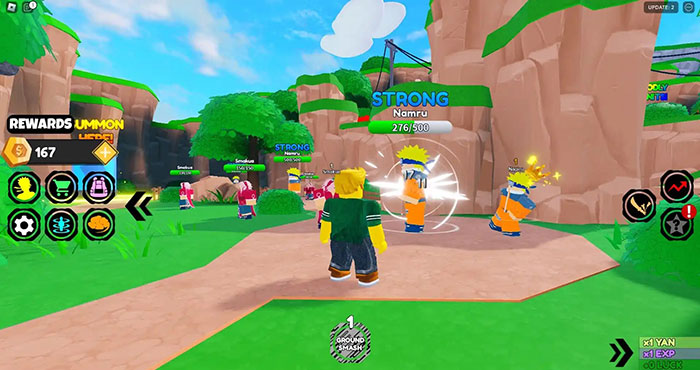
Khám phá code anime power simulator mới nhất và cách nhập code anime power simulator
Share Code
September 6, 2023
Bạn muốn khám phá code anime power simulator mới nhất và cách nhập code anime power simulator? Anime Power Simulator…

Khám phá code anime pet fighters simulator mới nhất và cách nhập code anime pet fighters simulator
Share Code
September 6, 2023
Bạn đã từng nghe về code Anime Pet Fighters Simulator mới nhất không? Bạn muốn tìm hiểu về mã nhập…

Khám phá code anime ninja war tycoon mới nhất và cách nhập code anime ninja war tycoon
Share Code
September 6, 2023
Bạn đã từng muốn trở thành một ninja mạnh mẽ và tham gia vào cuộc chiến ninja độc đáo? Với…

Khám phá code anime mania mới nhất và cách nhập code anime mania
Share Code
September 6, 2023
Bạn đã từng nghe về code Anime Mania chưa mới nhất? Đây là trò chơi hấp dẫn dành cho các…
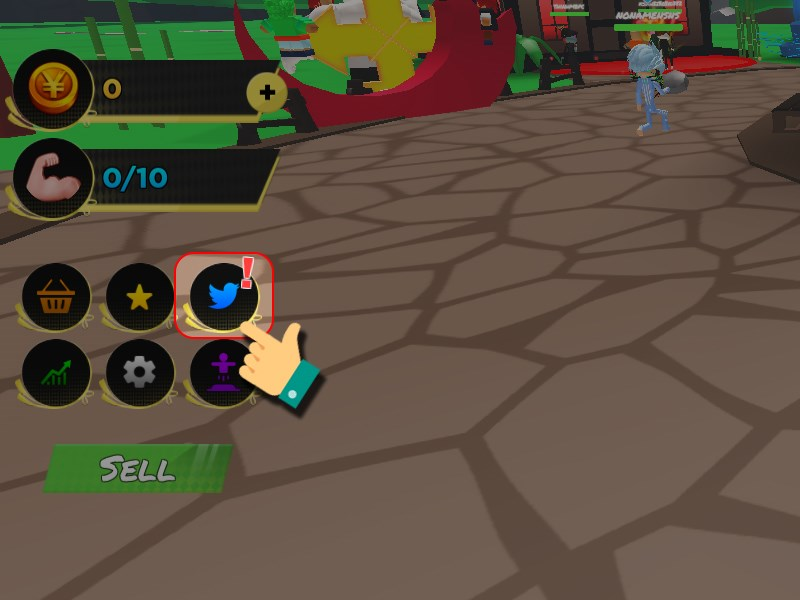
Tìm hiểu code anime lifting simulator Mới Nhất và cách nhập code anime lifting simulator
Share Code
September 6, 2023
Bạn muốn tìm hiểu về code anime lifting simulator mới nhất và cách nhập code trong trò chơi này? Bạn…

Code anime journey Mới Nhất – Nhập code nhận quà KHỦNG
Share Code
September 6, 2023
Khi tham gia tựa game Anime Journey trong bộ game Roblox, bạn sẽ có cơ hội nhập vai thành anh…

Code anime impact simulator Mới Nhất và cách nhập code
Share Code
September 6, 2023
Để nhận được Mana Multiplier bổ sung, bạn có thể đổi thẻ để mở khóa ngay lập tức những nhân…

Tập hợp mã Code Anime Hero Anh Hùng Loạn Chiến Mới Nhất năm 2023.
Share Code
September 6, 2023
Code Anime Hero Anh Hùng Loạn Chiến Mới Nhất là một trò chơi idle vừa được ra mắt gần đây,…

Tập hợp các code anime guardian Mới Nhất năm 2023.
Share Code
September 6, 2023
Khi bạn tham gia trò chơi Anime Guardian, bạn sẽ có cơ hội nhập vai vào nhân vật anime mà…

Tổng hợp code anime fruit simulator Mới Nhất năm 2023 và cách nhập
Share Code
September 6, 2023
Mẹo nhỏ cho các game thủ yêu thích anime fruit simulator! tamquoccola đã tổng hợp dành cho các bạn danh…

Code anime fighting simulator Mới Nhất năm 2023
Share Code
September 6, 2023
Anime Fighting Simulator là một trò chơi trong hệ thống Roblox, lấy cảm hứng từ nhiều bộ anime nổi tiếng.…

Anime Evolution Simulator là một trò chơi chiến đấu và thu thập trên nền tảng Roblox. Trong trò chơi này,…

Code anime dimensions simulator Mới Nhất năm 2023
Share Code
September 6, 2023
Code anime dimensions simulator Mới Nhất là một trong những tựa game Roblox nhập vai thú vị được nhiều bạn…
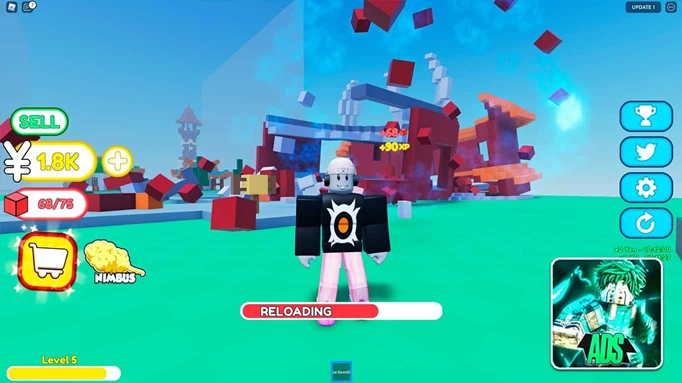
Code anime destruction simulator Mới Nhất 2023 – Cách nhập code
Share Code
September 6, 2023
Tựa game “Code anime destruction simulator Mới Nhất 2023” đang thu hút sự chú ý của cộng đồng game thủ…

Cách tìm và nhập code Anime Destroyers Simulator mới nhất
Share Code
September 6, 2023
Bạn có đam mê với việc tiêu diệt kẻ thù và muốn trải nghiệm những trận chiến hấp dẫn? Thì…
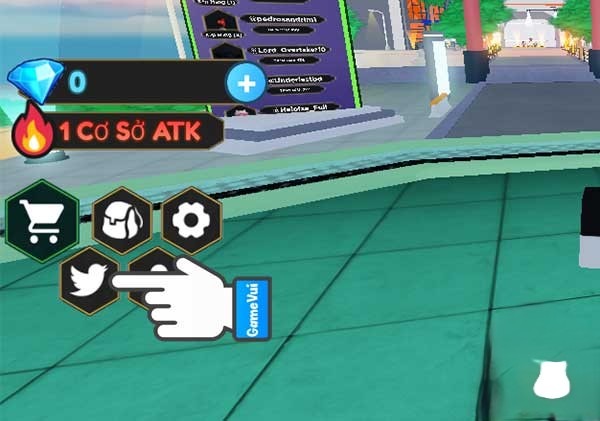
Cách nhập và đổi code Anime Defense Simulator mới nhất
Share Code
September 6, 2023
Hướng dẫn nhập và đổi code Anime Defense Simulator mới nhất! Tận hưởng những phần thưởng miễn phí và đá…
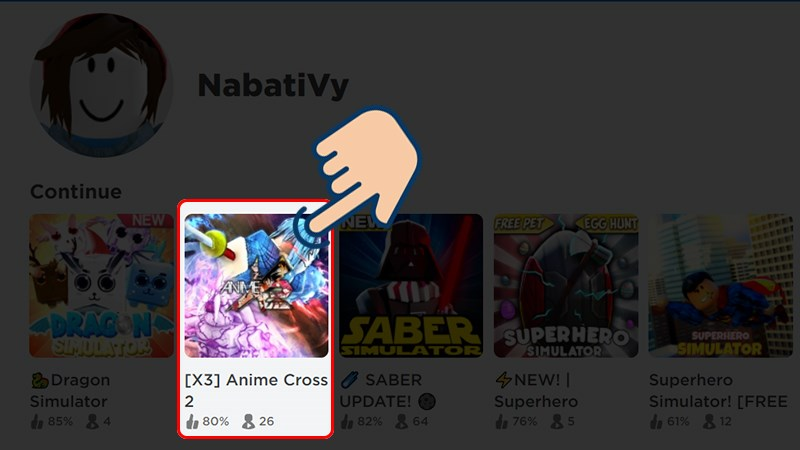
Roblox: Tổng hợp Mã code Anime Cross 2 và hướng dẫn sử dụng
Share Code
September 6, 2023
Anime Cross 2 là một trò chơi Roblox hấp dẫn, mang phong cách anime quen thuộc nhưng có lối chơi…

Danh sách mã code Anime Clicker Fight mới nhất và cách nhập vào trò chơi
Share Code
September 6, 2023
Hãy khám phá danh sách mã code Anime Clicker Fight mới nhất của trò chơi và cách dễ dàng nhập…
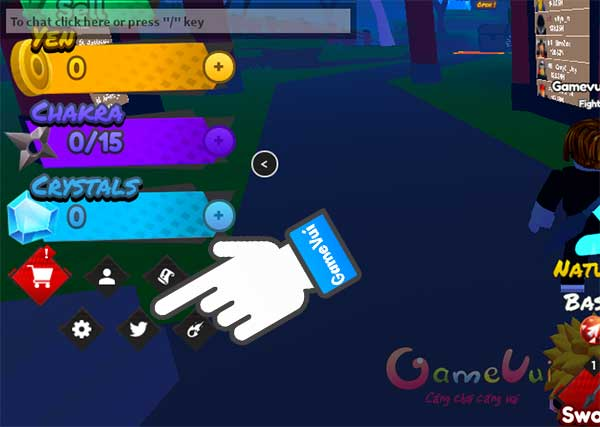
Mã code Simulator Anime Clash mới nhất và hướng dẫn sử dụng
Share Code
September 6, 2023
Mã code Anime Clash Simulator mới nhất và hướng dẫn sử dụng: Bạn đã chơi trò chơi click chuột trên…
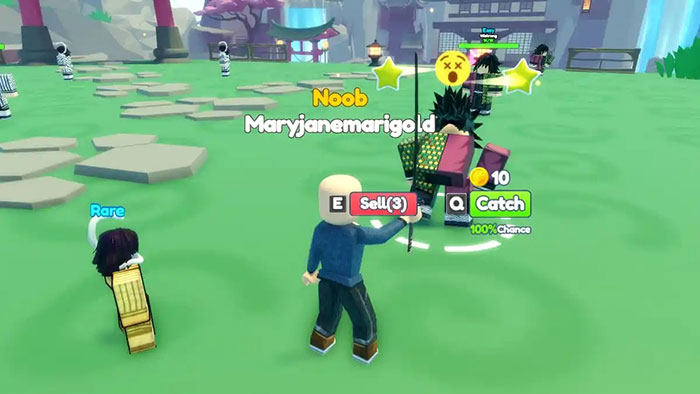
Cập nhật danh sách code Anime Catching Simulator mới nhất và hướng dẫn cách nhập
Share Code
September 6, 2023
Anime Catching Simulator là một trò chơi Roblox thú vị dành cho những người yêu thích Pokémon và việc bắt…

Cách tìm mã code Anime Brawl ALL OUT mới nhất
Share Code
September 6, 2023
Bạn đang tìm kiếm những cách để nâng cao khả năng chiến đấu và tích luỹ tài nguyên trong thế…
Danh sách mã code Anime Battlegrounds X mới nhất: Hướng dẫn cách nhập code
Share Code
September 6, 2023
Bạn đã nghe đến danh sách mã code Anime Battlegrounds X mới nhất chưa? Hãy khám phá cách nhập code…
Hướng dẫn cách nhập code Anime Attack Simulator mới nhất
Share Code
September 6, 2023
Những mã code Anime Attack Simulator mới nhất giúp tăng sức mạnh, tăng tiền và tăng đá quý cho người…